Cette expression est employée dans le premier chapitre de l’excellent ouvrage « l’Harmonie » de Jean-Louis Fabre. Il y explique que la théorie de la musique tonale est basée sur un phénomène physique, les harmoniques d’un son. Je vais ici essayer de l’illustrer, de le rendre palpable.
Tout d’abord, trouvons un « son ». J’ai une guitare sous la main, je filme l’action de mon doigt sur la grosse corde, au milieu de la corde, là où ça vibre le plus :
Ce son, c’est un mi. Il s’écrit comme ça sur une partition de guitare :

Ce mi est provoqué par la vibration de la corde, qui fait vibrer l’air, qui fait vibrer notre tympan, pour que notre cerveau entende un mi. La hauteur de la note correspond à une fréquence de vibration de la corde.
Cherchons la fréquence de notre mi dans cette table de wikipedia. C’est facile, la dernière colonne c’est les notes des cordes de la guitare (open strings). En anglais « mi » c’est « E », « low » car corde grave :

Donc notre mi vibre à une fréquence de 82.4069 Hertz. C’est à dire que la corde fait 82 aller retours par seconde.
Pour vérifier ça, je vais utiliser un outil fabriqué dans le Beaujolais. C’est un oscillateur-filtre-spectromètre tout en un. La première chose qu’on va faire, c’est simuler le son avec un oscillateur qui va générer une sinusoïdale de 82.4 Hz. La sinusoïdale est la forme qui donne le son le plus « pur ». Je vous fais ça en live, je choisis la forme sinusoïdale, règle la fréquence, et go :
Pas convaincu que c’est la même note ? Je mets le son sinusoïdal en fond, et le son guitare par dessus :
Mieux ? Ce n’est pas facile à entendre, ça demande un entraînement de l’oreille. Certains surhumains qui ont ce qu’on appelle « l’oreille absolue », entendent cette vibration en dehors de tout contexte et savent que c’est un mi. Pour les autres ils en sont réduits à comparer à une autre note.
D’un côté on a ce son artificiel qui ne contient que du 82 Hz, et de l’autre une corde, tenue par des bouts d’os (chevalet d’un côté, sillet de l’autre), attaquée par mon gros doigt rugueux, qui fait vibrer la table en bois, résonne dans la caisse, ressort par la rosace… Dans tout ce chemin se créent des harmoniques, des vibrations à d’autres fréquences.
On appelle « harmoniques naturelles » celles qui sont provoquées par la fréquence de base. Pour simuler ça, on va demander à notre oscillateur une onde triangle. C’est une manière artificielle de créer un son plus complexe, qui donnera un son plus proche de notre guitare que la sinusoïdale, même si on en est encore très loin.
On peut faire un parallèle avec les ondes de l’eau, en observant une goutte d’eau tomber dans l’eau :

C’est proche d’une onde sinusoïdale. Une onde triangle ce serait plutôt :
Je refais ça en direct avec l’oscilateur, et on va observer la courbe en bas à droite, qui donne la puissance de chaque fréquence :
Je n’ai changé que la forme de l’onde, triangle ou carrée, mais au niveau des fréquences tout est chamboulé ! Ces sont les harmoniques. On va maintenant utiliser le curseur en haut à droite, qui est un filtre biquadratique (je ne sais pas exactement ce que ça veut dire, mais c’est facile à utiliser), qui permet de choisir une fréquence, un gain et une largeur. Donc d’amplifier une plage de fréquences. Écoutons, c’est visuel :
J’ai cherché les fréquences de ces harmoniques que l’on voit, les sommets des bosses. J’ai trouvé ceci pour les trois premières fréquences
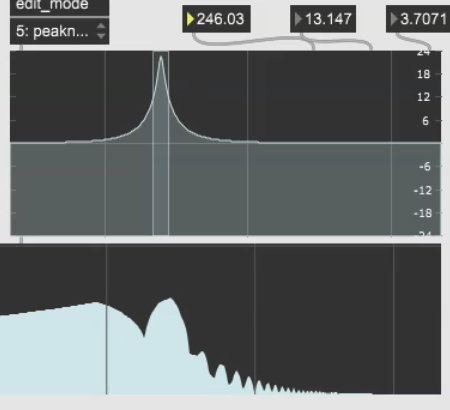
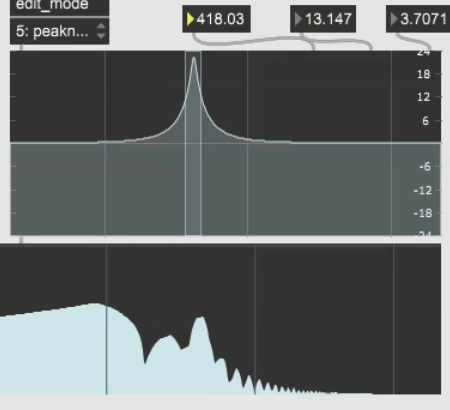
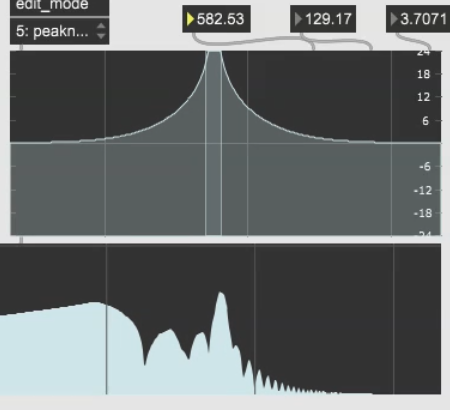
On note les fréquences : 246, 418, 582.
Et on se dit que ces fréquences pourraient être des fondamentales d’autres notes. On reprend le tableau qu’on avait plus haut, pour voir si ça tombe sur des notes de musique.



Bingo ! A 3 ou 5 Hertz près, on tombe sur : si (B), sol# (G#) et ré (D). Par rapport au mi, le si correspond à la quinte (avec les doigts : mi, fa, sol, la, si, 1 2 3 4 5, quinte), le sol à la tierce majeure (mi fa sol), et le ré à la septième mineure (mi fa sol la si do ré).
C’est l’accord de dominante ! Soit l’épicentre de l’harmonie tonale. Si on le note pour guitare :

En jouant l’accord de grave vers aigu, cela nous donne :
Je n’ai pas pu m’empêcher en jouant cet accord, ça sonne comme… le blues ! Je n’avais pas de conclusion prévue, mais la voici : les harmoniques d’un son sont la racine du blues. Et avant, de l’harmonie tonale.
Références
- L’outil a été développé avec Max 8, un produit de Cycling ’74/IRCAM
- Les notes sont écrites avec Lilypond
- La guitare est enregistrée par mes soins
- Le tableau des fréquences des notes vient de Wikipedia
- Les photos d’eau d’une recherche internet
2 commentaires